Interpretability in Black Box Machine Learning Methods
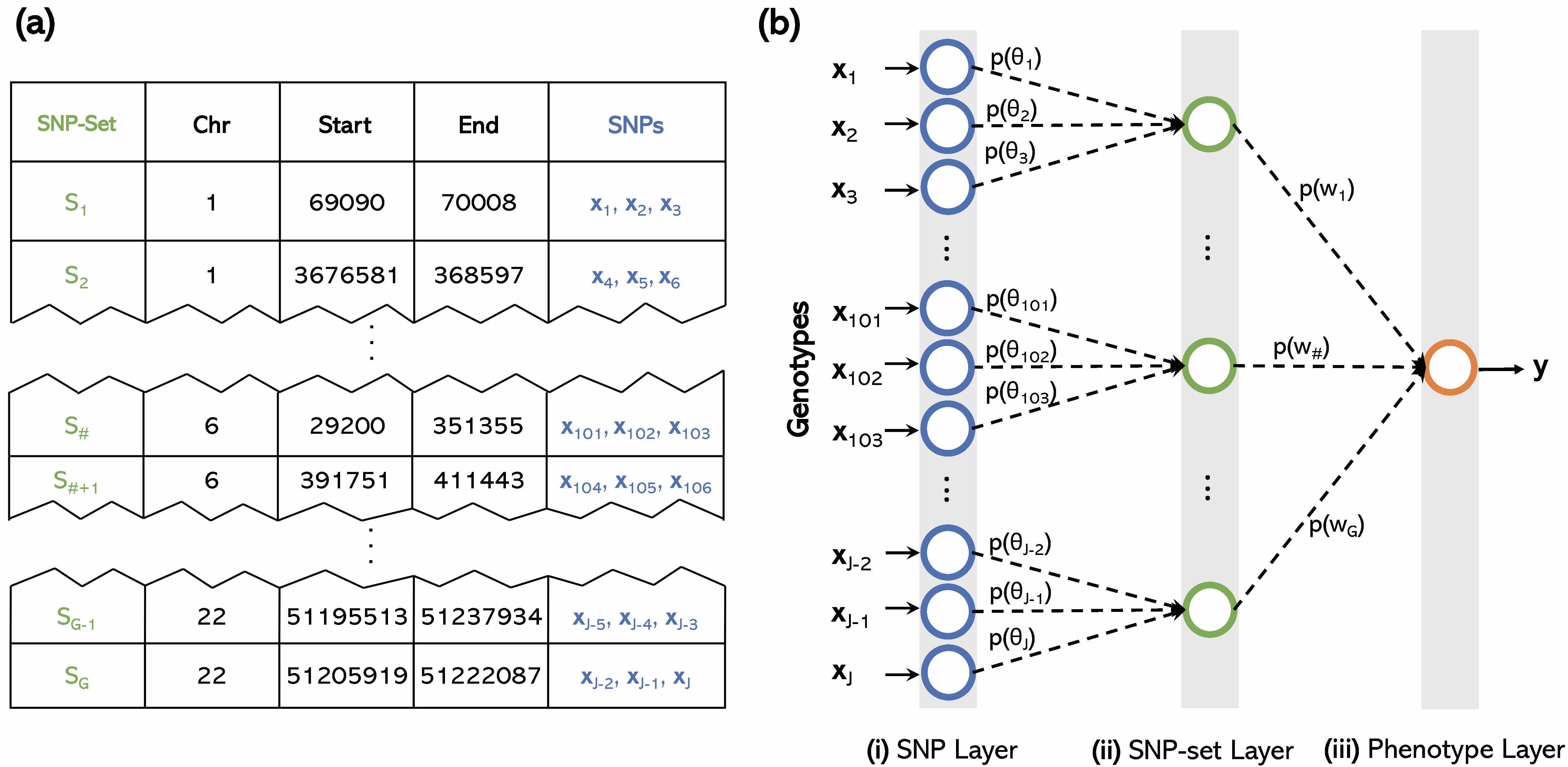
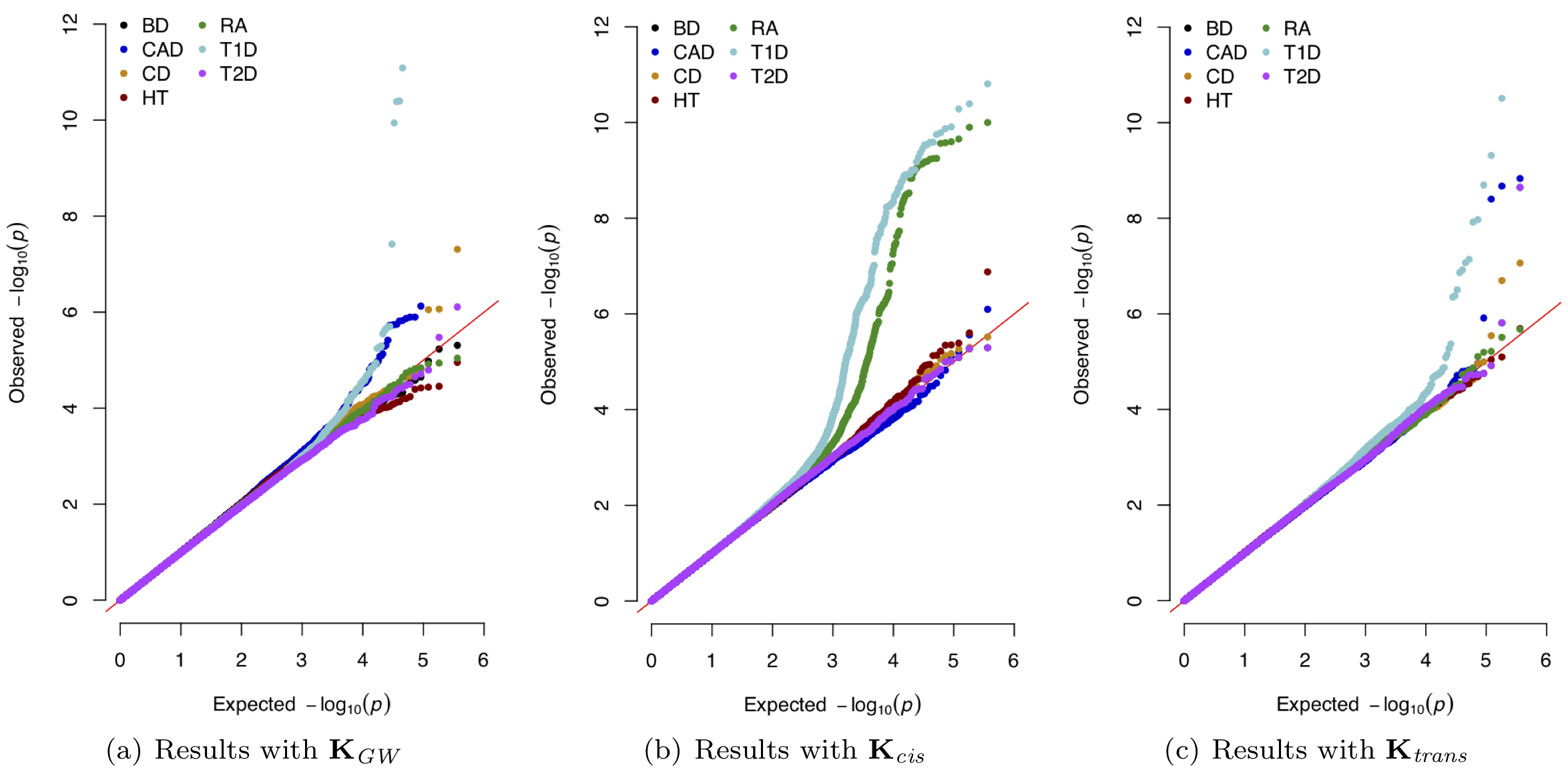
Nonparametric regression models are often used in statistics and machine learning due to greater predictive accuracy than linear models. Variable selection for these nonlinear methods, however, is a challenge partly because, unlike the linear regression setting, there is no clear concept of an effect size for regression coefficients. From a conventional genetics perspective, this may be alternatively explained as two key distinct problems: genomic selection (predicting phenotype from genotype) and association mapping (inference of significant variants or loci). State-of-the-art methods for genomic selection and association mapping are based on nonparametric regression and linear models, respectively. Using functional analytic properties of reproducing kernel Hilbert spaces (RKHS), we work to develop novel methods that both (1) capture nonlinear structure and (2) can provide interpretable significance measures for each of the original explanatory (or input) variables. This results in the first unified frameworks that are competitive in association mapping, phenotypic prediction, and sample classification. We provide publicly available packages (e.g., Biologically Annotated Neural Networks; BANNs) for implementing these types of methods.
Methods for Identifying Statistical Epistasis
Epistasis, commonly defined as the interaction between multiple genes, is an important genetic component underlying phenotypic variation. Many statistical methods have been developed to model and identify epistatic interactions between genetic variants. However, because of the large combinatorial search space of interactions, most epistasis mapping methods face enormous computational challenges and often suffer from low statistical power due to multiple test correction. We develop novel methods and algorithms that take significant steps towards solving the cost and throughput limitations associated with the study of interactions in genetic association studies. We work to facilitate the detection of epistasis, all while alleviating much of the statistical and computational burden associated with standard epistatic mapping procedures.
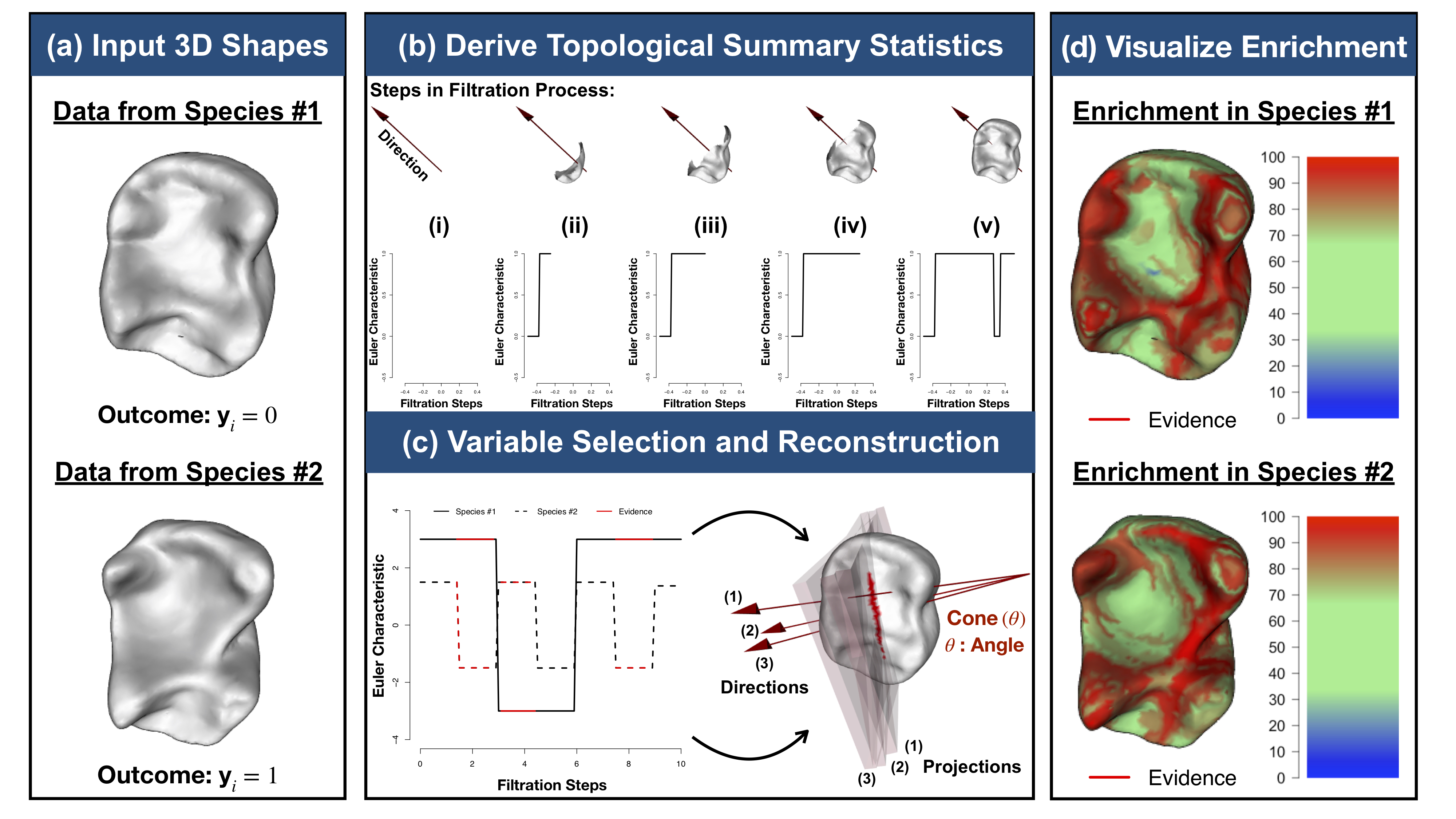
Modeling Variation in 3D Shapes using Topological Summary Statistics
In recent decades, there have been major developments in integrating shape analyses with statistics on multiple fronts. However, in spite of these advances, there still exist many barriers in attempts to develop principled and computationally feasible approaches to effectively analyze 3D shapes of diverse geometry and topology. With active collaborations with many experts in mathematics and physics, we are working to develop functional data analytic methods that generalize the use of topological summaries in statistics and regression techniques. Radiomics, which focuses on understanding the relationship between clinical imaging and functional genomic variation, is a natural application area.
Statistical Methods for Pharmacology and Cancer Biology
Targeted therapies aimed to inhibit oncogenic signaling within many cancer subtypes have been proven to have high initial clinical responses, but relapse in these patients is almost inevitable. While the genetic alteration of numerous cytoplasmic proteins and pathways can drive acquired resistance to certain inhibitors, a central open question in the field is whether these diverse alterations lead to common or divergent biological programs. To better address these questions computationally, we develop methods and algorithms that define rigorous transcriptional signatures of cancer recurrence and therapeutic resistance. With our collaborators, we not only work to define the key transcriptional outputs of cellular pathways, but also work to suggest more robust and universal strategies for treating resistant tumors of all tissues types.